Algorithme de Farey

---

Soit $T : \mathbb R_+^2 \to \mathbb R_+^2$ définie par

$T(x_a,x_b) = \begin{cases} (x_a, x_b-x_a) &\textit{si } x_a < x_b\\ (x_a-x_b, x_b) &\textit{si } x_a > x_b \end{cases}. $

On étiquette chacun des cas par la lettre qui $\textit{perd}$.
Ce qui associe à chaque vecteur de $\mathbb R_+^2$ un chemin dans le graphe suivant.

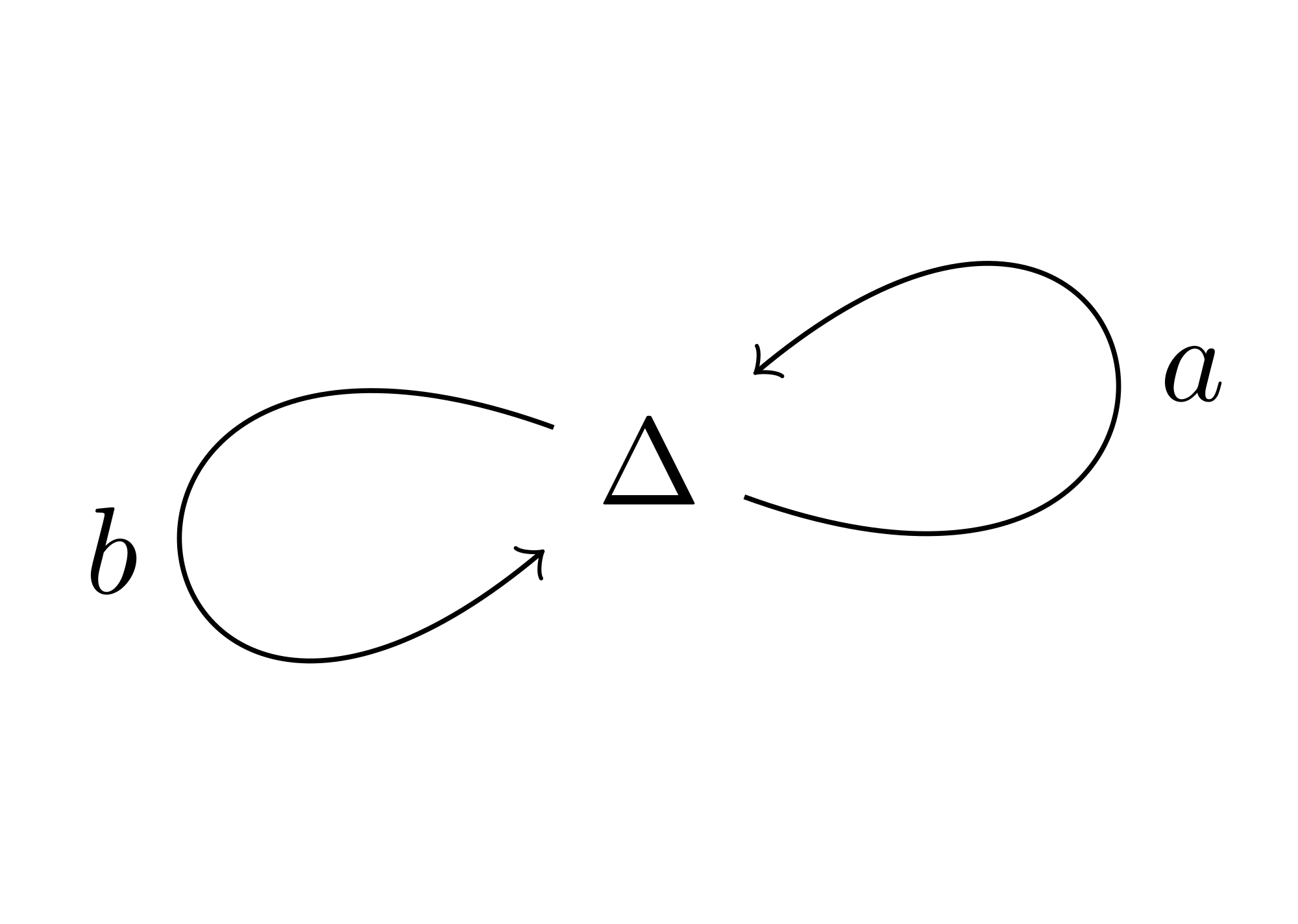
Cette fonction est invariante par multiplication par un scalaire strictement positif.
On peut donc se ramener à son étude sur un domaine fondamentale donné par l'intersection d'une droite avec le cône.

from farey import *
cone()

Remarque

Pour un $\color{red}{x} \in [0,1]$ choisi selon la loi de probabilité uniforme, on peut associer le codage $$\color{red}{aaabaabbba \dots}$$ C'est une marche aléatoire dans le graphe.

Il serait utile de pouvoir décrire la loi de probabilité de la prochaine lettre sachant le début du codage.

Exemple

On préfère souvent penser au développement binaire d'un nombre aléatoire comme un mot tiré avec une loi de Bernoulli sur $\{0,1\}^{\mathbb N}$.

Question

Si l'on sait que le codage de $\color{red}{x}$ commence par $\color{red}{aaaaaaa}$, quelle est la probabilité que la prochaine lettre soit $\color{red}{a}$ ?

Même question pour $\color{red}{aaaaaaab}$ ?

Mesure sur le domaine fondamental

---

Pour $q \in (\mathbb R_+^2)^*$ on définit un domaine fondamental du cône par le simplexe

$\Delta(q) = \left\{ \mathbf x \in \mathbb R_+^2 \mid \langle q, x \rangle = 1 \right\}$

et le cône sous ce domaine

$\Lambda(q) = \left\{ \mathbf x \in \mathbb R_+^2 \mid \langle q, x \rangle \le 1 \right\}$.

Il existe une mesure naturelle associée pour $U \subset \Delta(q)$

$\nu_q(U) = Leb \left( \Lambda(q) \cap \mathbb R_+^2 U \right)$ .

---

C'est la mesure de Lebesgue sur l'intervalle $\Delta(q)$.

Mesure conditionnée à l'étape passée

Soit $T_a = T_{|x_a < x_b}$ et $T_b = T_{|x_a > x_b}$.

Remarquons que

$T_a = \left(\begin{array}{rr} 1 & 0 \\ -1 & 1 \end{array}\right) $ et $T_a^{-1} = \left(\begin{array}{rr} 1 & 0 \\ 1 & 1 \end{array}\right) =: M_a $

$T_b = \left(\begin{array}{rr} 1 & -1 \\ 0 & 1 \end{array}\right) $ et $T_b^{-1} = \left(\begin{array}{rr} 1 & 1 \\ 0 & 1 \end{array}\right) =: M_b $

Ainsi $ \nu_q ( U \mid a ) = \nu_{q M_a} (U) $ et $ \nu_q ( U \mid b ) = \nu_{q M_b} (U) $

En effet $\left( T_{a *} \nu_q \right) (U) = Leb \left( \Delta(q) \cap M_a(\mathbb R_+^2 U) \right) = Leb \left( M_a^{-1}(\Delta(q)) \cap \mathbb R_+^2 U \right) = \nu_{q M_a} (U) $

Car $M_a^{-1}(\Delta(q)) = \left\{ \mathbf x \in \mathbb R_+^2 \mid \langle q, M_a x \rangle = \langle q M_a, x \rangle = 1 \right\} = \Delta(q M_a)$

graphics_array([cone(), cone("a"), cone("b")]).show(figsize=[10,10])

animated_farey("aaab")

Dans le cas $a$, soit $q' = q M_a$, alors

$q'_a = q_a + q_b$ et $q'_b = q_b$

et de même dans le cas $b$, soit $q' = q M_b$, alors

$q'_a = q_a$ et $q'_b = q_b + q_a$

---

La proportion de chaque domaine est donnée par

$P(a) = \frac {q_a} {q_a + q_b}$ et $P(b) = \frac {q_b} {q_a + q_b}$

graphics_array([cone(), cone("aaa"), cone("aaab")]).show(figsize=[10,10])

Les probabilités de $a$ et $b$ dans chacunes de ces trois étapes sont données par

$\hspace{1cm} (\frac 1 2, \frac 1 2) \hspace{2cm} (\frac 4 5, \frac 1 5) \hspace{2cm} (\frac 4 9, \frac 5 9)$

Suspension canonique

---

Il existe une semi-flot de suspension canonique de l'algorithme de Farey projectivisé grâce à sa description dans le cone positif.

from farey import *
plot_flow_above()

xp, yp = rauzy_not(x,y)
graphics_array([plot_rauzy_above(x,y,0), plot_rauzy_above(x,y,1), plot_rauzy_above(xp,yp,0)]).show(figsize=[10,10])

cf = continued_fraction([(),(3,1,1,2)])
x,y = 1, cf.value().n()
rauzy_suspension_above(x,y,7)